كتابة: الأستاذة لينة
مراجعة: فارس بوخمسين
قد تأتي بعض الأيام التي يتمنى فيها أحدنا أن يمكن من الرجوع بالزمن إلى الوراء، ربما لتصحيح خطئٍ ارتكبه، أو للقاء عزيزٍ على القلب خطفه منه الزمن، أو ربما لتكرار عيش لحظاتٍ سعيدةٍ. إلا أننا ندرك أن هذا غير ممكنٍ وربما غير منطقيٍ بالرغم من أمنياتنا تلك!
كان البشر يعتقدون أن الزمان مطلقٌ ولا يتأثر بما يجري من حوله، فهو ما يغيِر ولا يُغيَّر. ولكن هذا ليس صحيحاً تماماً، فلقد مزقت النظرية النسبية العامة تلك الرؤية السرمدية والفلسفية للزمان إرباً إرباً قبل 100 عامٍ من اليوم! فالزمان مرنٌ ويتأثر بالمادة وينحني وربما يلتف أيضاً، ويعتمد على الراصد وبعيد كل البعد عن كونه مطلقاً. تلك الحقيقة العلمية أصبحت أمراً مفروغاً منه، ولم يعد الجدل حولها ذو جدوى. فالزمن لم يعد أمراً فلسفياً أو شاعرياً، بل دخل مختبرات العلم وألواح النظريين السوداء التي تكسوها الطباشير بدلاً من أن يكون بمتناول أقلام الأدباء والشعراء والفلاسفة!
في شهر نوفمبر من سنة 1915مـ، نُشِرت ورقةٌ بحثيةٌ غيرت الفيزياء رأساً على عقب، ألا وهي نظرية النسبية العامة للفيزيائي النظري ألبرت اينشتاين. إن النسبية العامة نظريةٌ هندسيةٌ للجاذبية، والتي تقوم على أساس التكافؤ العام بين الراصدين المتسارعين تسارعاً منتظماً وأولئك الواقعين تحت تأثير الجاذبية. وتبين أن الزمكان (الزمان والمكان) نسيجٌ واحدٌ لا يمكن الفصل بينهما كما عهدنا سابقاً، كما أنهما مرنين وقابلين للإنحناء (*) تحت تأثير المادة والطاقة، مفسرةً بذلك تفاعل الجاذبية على أنه تغيرٌ بالهندسة الداخلية للزمكان. ومن هنا يجب التنويه أن “الهندسة الداخلية” هي خاصيةٌ ذاتيةٌ بالزمكان ومقارنتها بغشاءٍ منحنٍ بشكلٍ خارجيٍ تشبيه مجحفٌ وبعيدٌ عن الدقة.
إن النسبية العامة نظريةٌ ناجحةٌ للغاية عند تطبيقها على المسائل الفلكية مثل مسارات الكواكب وغيرها من الأجرام السماوية، بالإضافة إلى حساب تباطؤ الزمن بالقرب من سطح الأرض (نظراً لزيادة شدة مجال الجاذبية)، وهو حسابٌ ذو أهميةٍ قصوى بالنسبة لنظام تحديد المواقع العالمي. ولكن معادلات حقل أينشتاين(**) الخاصة بالنسبية العامة تخفي بين رموزها الكثير من المعضلات، وربما تحمل معها أحلام الطامحين بـ” آلة الزمن”.
إن النسبية العامة نظريةٌ توبولوجيةٌ(***)، وبالتالي إن كنت جيداً بتصور توبولوجيا الزمكان فبإمكانك خلق حلولٍ لمعادلات الحقل لنوعٍ محددٍ من المادة وبترتيبٍ معينٍ تستطيع به تحقيق التوبولوجيا التي تتصورها مبدئياً، وربما لن تستطيع. ولهذا فإن الزمكان كما تصفه بعض معادلات الحقل لا تسمح بها الفيزياء، ولا توجد حتى المادة التي تحتاجها. ومن تلك التوبولوجيات التي نريد التأكد من خلو الزمكان منها هي توبولوجيات آلات الزمن، أو ما تسمى بالمنحنيات الزمانية المغلقة، فتلك التوبولوجيات تخرق مبدأ السببية الذي يبدو منطقياُ للغاية وواضحاُ، والذي ينص باختصار على:
“لكي يكون لأي حدثين علاقةٌ سببيةٌ، أيّ أن أحدهما سبب بالآخر، يجب أن يقعا ضمن المخروط الضوئي(+) لبعضهما، كما يجب أن يسبق المسبب السبب زمنياً.”
إن الشرط الأول يعني بأن من غير الممكن لأي إشارةٍ أن تسبق سرعة الضوء (#)، أما الثاني فهو واضحٌ: يجب أن يأتي المسبب قبل السبب، وإلا فلا معنى للسببية!
أما في المنحنيات الزمانية المغلقة فمستقبل الجسيم أو الراصد يقع في ماضيه، ولهذا يختل مبدأ السببية تماماً ويختل مفهومنا لتتابع الأحداث بالكلية! فلنأخذ مثالاً على ذلك:
لنقل إنك دخلت في منحنىً زمانيٍ مغلقٍ وكان وقت دخولك في الساعة الثانية ظهراً، وبعد أن أتممت دورةً كاملةً في هذا المنحنى ستشير ساعتك إلى السادسة مساءً، ولكنك ستكون حينها قد عدت إلى “الماضي” أو إلى الزمكان حيث كانت الساعة الثانية ظهراً في اليوم السابق (لأن الوقت عند الراصد يجري بمعدلٍ ثابت، بينما يعود على نفسه)، وإن أتممت دورتين ستكون قد عدت إلى الماضي أكثر وهكذا.
إن المنحنيات الزمانية المغلقة وصفٌ علميٌ للسفر “للماضي”، ولكن لا يمكن وصفها بالسفر عبر الزمن هنا، لأننا جميعاً نسافر عبر الزمن ولكن “باتجاهٍ واحدٍ” فقط. أما في المنحنيات الزمانية المغلقة فسيكون هذا الاتجاه معكوساً.
إن السببية وتتابع الأحداث أمران هامين للغاية بالطبع، فلولاهما ستحدث الكثير من التناقضات المنطقية مثل أن ترجع بالزمن للوراء قبل أن ينجب جدك أباك ثم تقتله، حينها من أنجبك أنت؟ وإن أردنا وصفاً علمياً ودقيقاً أكثر، فإن الإخلال بتتابع الأحداث سيؤدي لخرق قوانين الحفظ الأساسية في الفيزياء، مثل حفظ الطاقة والشحنة في الكون في كل لحظةٍ زمنيةٍ ($).
إذاً، نحتاج لأن نمنع تكون تلك الزمكانات الخطيرة المثيرة للجدل، ولكن النسبية العامة تظهرها ولا تمنعها. كما يمكن العثور على حلولٍ لمعادلات الحقل والتي تسمح بتكون منحنياتٍ زمانيةٍ مغلقةٍ، ومن تلك الحلول وأولها حل كيرك جوديل للكون الساكن والذي لا يتوسع ولكنه يدور وله ثابتٌ كونيٌ. حل جوديل هذا يتنبأ بوجود منحنياتٍ زمانيةٍ مغلقةٍ في هذا الكون (الافتراضي) بسبب تأثيرٍ يسمى “جرّ المحاور”، حيث يؤدي انحناء الزمكان ودورانه أيضاً لجعل المخاريط الضوئية لبعض المراقبين “تميل” على جانبها بحيث يصبح اتجاه المستقبل بها متقاطعاً مع ماضيها. إن حل جوديل غير واقعيٍ لأن كوننا يتوسع ولا يحتوي على أي عزمٍ زاويٍ (لا يدور بالكلية أو يدور بسرعةٍ فائقة الضآلة)، ولكنه بالرغم من ذلك يطرح مشكلةً أو نقاشاً علمياً أساسياً لمسألة السفر إلى الماضي!
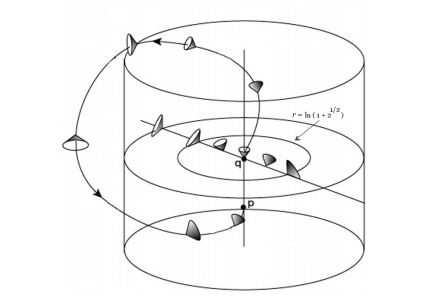
شكل 1: حل كيرك جوديل والمنحنيات الزمانية المغلقة
أتى حلٌ آخر يسمى بأسطوانة اللانهائية (أو الأسطوانة الطويلة بشكلٍ كبيرٍ)، والتي تمتلك مادةً ذات كثافةٍ عاليةٍ وتدور بسرعةٍ كبيرةٍ مكونةً نفس التأثير السابق في حل جوديل. حيث أن تسارع راصدٍ من المالانهاية إلى تلك الإسطوانة سيدخل في منحنياتٍ زمانيةٍ مغلقةٍ بالقرب منها، ولكن هذا الحل احتوى على مشاكل تحد كثيراً من أهميته، حيث تزداد كثافة المادة كلما كبر نصف قطر الإسطوانة، وهذا لا يحدث في المادة العادية، حيث تقل الكثافة كلما زاد الحجم مع ثبات الكتلة.
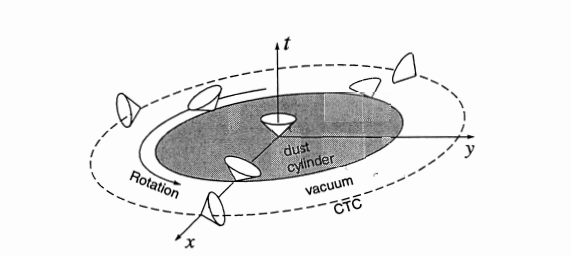
شكل 2: الزمكان في محيط اسطوانة تبلر
يكمن الجدل أيضا فيما إذا كانت هذه الاسطوانة لا نهائيةً أم متناهيةً. فالثقوب السوداء الدوارة (حل كير) توّلِد أيضاً منحنياتٍ زمانيةً مغلقةً، ولكن الأخيرة تقع ضمن أفق حدث الثقب الأسود. فإن دار الثقب الأسود بسرعةٍ كبيرةٍ سيؤول الحل لحل الأسطوانة السابقة، والتي اكتشف حلها فان ستوكوم واكتشف تبلر خصائصها بتكوين منحنياتٍ زمانية مغلقة، ولذلك تسمى بأسطوانية تبلر.
تبدو الحلول السابقة غير واقعيةً وبعيدةً عن أيّ تطبيقٍ ممكنٍ، ولكنها مهمةٌ في طرح الفكرة وكيف يمكن للنسبية العامة أن تسمح لوجود “آلات الزمن” من حيث المبدأ.
أتت حلولٌ أكثر أهميةً لاحقاً والتي تُعرف بالثقوب الدودية الناقلة، وسنتحدث عن الثقوب الدودية والفيزياء الخاصة بها في مقالٍ آخر لاحقاً.
من الحلول الأخرى لآلات الزمن هو زمكان مينسر، والذي يتمثل برقعةٍ من الزمكان تشابه تلك التي في لعبة باكمان الشهيرة، حيث إن انتهيت إلى حافة اللعبة ستخرج من الحافة المقابلة. هذا هو الحال تقريباً في فضاء مينسر، والذي إن تم تطبيقه على “حافةٍ زمنيةٍ” معينةٍ سيكون وجود آلة الزمن ممكناً. كما يوجد العديد من الحلول الآخرى التي ظهرت لاحقاً والتي أصبحت تعرف بـ”حلول آلات الزمن”.
لكن يبقى السؤال، هل تسمح قوانين الفيزياء بهذا؟
افترض ألبرت أينشتاين أن للمادة شروطاً معينةً لكي تسمح للفيزياء بوجودها، وتعرف هذه بشروط الطاقة (°). كما افترض أيضاً أن بالإمكان تجاوز تلك الزمكانات المثيرة للمتاعب بفرض شروط الطاقة تلك، ولكن ذلك لم ينفع. فنحن نعلم بوجود حالاتٍ تُخالف شروط الطاقة، مثل الفراغ بين لوحين قريبين من بعضهما (فراغ كازيمير). قام ستيفن هاوكينغ بفرض “حماية تسلسل الزمن” بافتراض بعض المسلمات القائمة على التحليل التوبولوجي وشروط الطاقة. ولن نخوض في تفاصيل حماية تسلسل الزمن بشكل تجريديٍ، ولكننا سنذكر بعض الأمثلة للتناقضات التي يمكن أن تمنع تكون آلات الزمن.
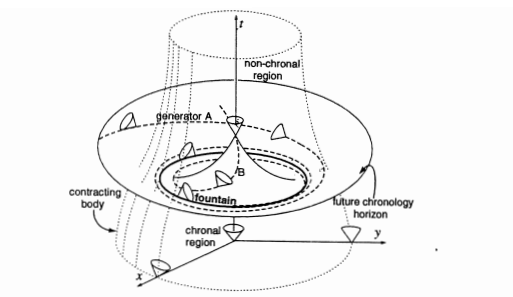شكل 3: استقرار حلول آلات الزمن باستخدام طاقة تنافي شروط الطاقة لتكون “نافورة” في مركز الحلول
أول تلك الأمثلة هي أفق الحدث للثقوب الدودية، والتي تُعالج بافتراض مادةٍ تخرق شروط الطاقة، وسنتحدث عن هذه الحالة في المقال الخاص بفيزياء الثقوب الدودية. ومن الافتراضات حول حماية تسلسل الزمن هي أنه لا يمكن لهندسةٍ محصورةٍ أن تنتج المنحنيات الزمانية المغلقة، وذلك مثل افتراض أن اسطوانة تبلر لا نهائية. ويمكن تجاوز هذه المعضلة بافتراض منطقةٍ “غير زمانيةٍ” مثل تلك التي في داخل الثقوب السوداء أو أن تكون المادة المكونة للأسطوانة خارقةً للشروط وتجعلها محدودة الطول والحجم.
من المعضلات أيضاً مسألة انبعاث موجةٍ كهرومغناطيسيةٍ ضمن زمكان مثل زمكان مينسر، حيث ستشهد تضخماً وانزياحاً نحو الأزرق بسبب هذه الهندسة، مما يؤدي بالنهاية لتكوّن ثقبٍ أسودٍ. تحدث الكثير من التناقضات عند دراسة نظرية الحقل الكمومي في تلك المنحنيات، مما يهدد الفيزياء كما نعرفها. ويصر ستيفن هاوكينج على أن نظرية الحقل الكمومي ستحد كثيراً من استقرار المنحنيات الزمانية المغلقة للغاية، مؤديةً إلى إنهيار تلك الزمكانات وبذلك تحفظ السببية والتسلسل الزمني.
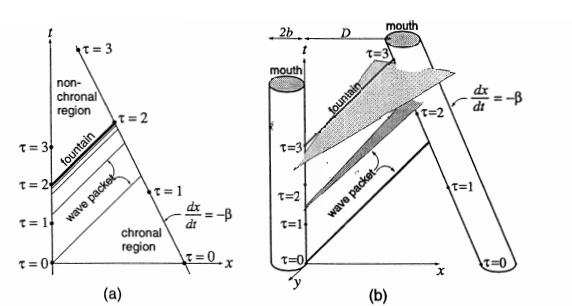
شكل 4: إنزياح الموجة الكهرومغناطيسية نحو الأزرق بشكل متزايد و”خارج عن السيطرة” في حل مينسر
بالرغم من هذا، لا يوجد إثبات رياضي شامل لفرض هاوكينج، كما أن بعض الزمكانات تبدو وكأنها مستقرةٌ بالنسبة لفرضية هاوكينج حول الأثار الكمومية. وسيبقى الجدل قائماً في إنتظار حسمه من نظرية جاذبية كمومية مكتملة!
(*): الإنحناء Curvature هي خاصية هندسية بالأسطح تعرف رياضيا بأنها فشل متجه يسير بمسار مغلق أن يعود إلى حالته الأصلية عند إكمال هذا المسار. فمثلا الكرة هي سطح منحني ثنائي الأبعاد.
(**): هي المعادلات التي تقوم عليها النظرية النسبية العامة، والتي يمكن من خلالها حساب انحناء الزمكان عند تواجد المادة أو الطاقة به.
(***): التوبولوجيا topology ، علم يدرس الأشكال والأسطح في الفراغ. النظريات التوبولوجية نظريات تفسر تغير الأشكال أو ديناميكا الأشكال تلك.
(+) المخروط الضوئي: مفهوم افتراضي أو تخيلي يشرح المنطقة من الكون التي يرتبط معها راصد سببياً.
(#): تعتبر سرعة الضوء هي السرعة القصوى، لا يمكن نقل أي إشارات بسرعة أكبر من سرعة الضوء. ونعرف المخروط الضوئي light cone بأنه جزء من الزمكان خاص بكل “راصدٍ” ويشمل جميع النقاط من الزمكان (الأحداث) التي يمكن لهذا الراصد أن يتواصل معها سببياً، أيّ يكون مسبباً لها أو أثراً منها.
($): تعرف هذه بقوانين الحفظ Conservation Laws ، والتي تترجم بلغة ميكانيك الكم / نظرية الحقول الكمومية بمفهوم الواحدية Unitarity
(°): شروط الطاقة Energy Conditions هي خصائص أو قيود معينة على طبيعة التنسور الخاص بالطاقة و الإجهاد Stress-Energy Tensor كي يمكن استخدام الأخير في معادلات حقل أينشتاين بصورتها التقليدية.
ملحق المصطلحات العلمية:
زمكان spacetime
منحنى زماني مغلق Closed Timelike Curve ( CTC)
ساكن Static / Stationary
ثابت كوني Cosmological Constant
عزم زاوي Angular momentum
جر المحاور Frame Dragging
راصد محور Observer/ frame
اسطوانة تبلر Tipler’s Cylender
ثقب أسود دوار / تقب كير الأسود Rotating Blackhole / Kerr Blackhole
ثقب دودي ( ناقل) : ( Transversable) Wormhole
حماية تسلسل الزمن : Chronology Protection Conjecture
تسلسل الزمن : Chronology
السببيبة Causality
الإنزياح نحو الأزرق Blue Shift ( Gravity)
محصور (توبولوجيا): Compact ( manifold )
فان ستوكوم van Stockum
مينسر Minser
باكمان Packman
المصادر:
