كتابة: عبدالحميد شكري.
قد يتساءل البعض: لم يعد قياس بعد الأجرام السماوية مهماً إلى هذا الحد؟ والإجابة على هذا السؤال هو أنه بما أن الضوء يسير بسرعة ثابتة (300 مليون م/ث)، فعلى سبيل المثال، يستغرق الضوء المنبعث من الشمس قرابة 8 دقائق ليصل إلينا، أي أننا نرى الشمس كما لو كانت عليه قبل 8 دقائق تقريباً. وبما أن المجرات تبعد ملايين بل ومليارات السنين الضوئية، فرصدها يعد بمثابة النظر إلى ماضي الكون، إذ يحاول الفلكيون بذل قصارى جهدهم لفهمٍ أفضل للكون عن طريق المعلومات التي نستقبلها من الضوء الصادر من أعماق الكون.
إذاً كيف يقيس الفيزيائيون أبعاد الأجرام السماوية؟
1- انعكاس موجات الرادار:
إن أول وأكثر الطرق دقة لقياس المسافات في الفضاء هي عن طريق رصد الموجات المرتدة من الجسم إلى الرادار. تعد هذه الطريقة دقيقة جدا لدرجة أنها مكنتنا من قياس الوحدة الفلكية و.ف. (وهي متوسط المسافة بين الأرض والشمس) إلى خانتين بعد الفاصلة (1 و.ف. = 149,597,870.61 كم). تعمل هذه الطريقة كالتالي، يقوم الفلكيون بإرسال نبضة لاسلكية بواسطة الرادار وعندما تصطدم تلك النبضة بالهدف يرتد جزء منها ليتم رصدها عند عودتها من الهدف وحساب زمن عودتها. وباستخدام المعادلة التالية يمكن حساب مسافة الهدف:
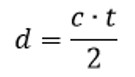
حيث c هي سرعة النبضة وهي نفس سرعة الضوء، t هي زمن الرحلة التي استغرقتها الموجة (ذهابا وإيابا) ولهذا تمت قسمتها على 2 لحساب زمن اتجاه واحد، و d هي المسافة المراد حسابها من الهدف (شكل 1).
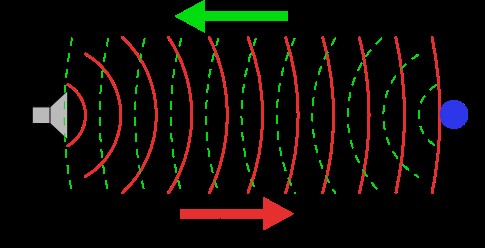
شكل 1: انعكاس موجات الرادار.
إلا أن هذه الطريقة تعد محدودة داخل مجموعتنا الشمسية فقط، فبعد مسافة 10 و.ف تقريبا تصبح الموجات المرتدة باهتة جدا ويستحيل رصدها، لذا يلجأ الفلكيون إلى الطريقة التالية.
2– التخاطل الرياضي:
تعد فكرة التخاطل بسيطة للغاية، فعندما تقوم بمد يدك ورفع إبهامك وتغلق إحدى عينيك ثم تفتحها وتغلق الأخرى وتعاود الكرة مرارا وتكرارا ستجد أن إبهامك يتحرك يمينا ويسارا. هذا بالضبط مايحدث مع فكرة التخاطل إلا أن الفلكيين يستخدمون بدلا من ذلك نصف مسار حركة الأرض حول الشمس (على مدار ستة أشهر)، حيث يتم رصد نجم في فصل الصيف مثلا ثم يتم رصده مرة أخرى في فصل الشتاء ويقومون بقياس زاوية التخاطل ليتمكنوا باستخدام علم المثلثات من حساب المسافة إلى النجم وفقا للمعادلة التالية: (شكل 2)
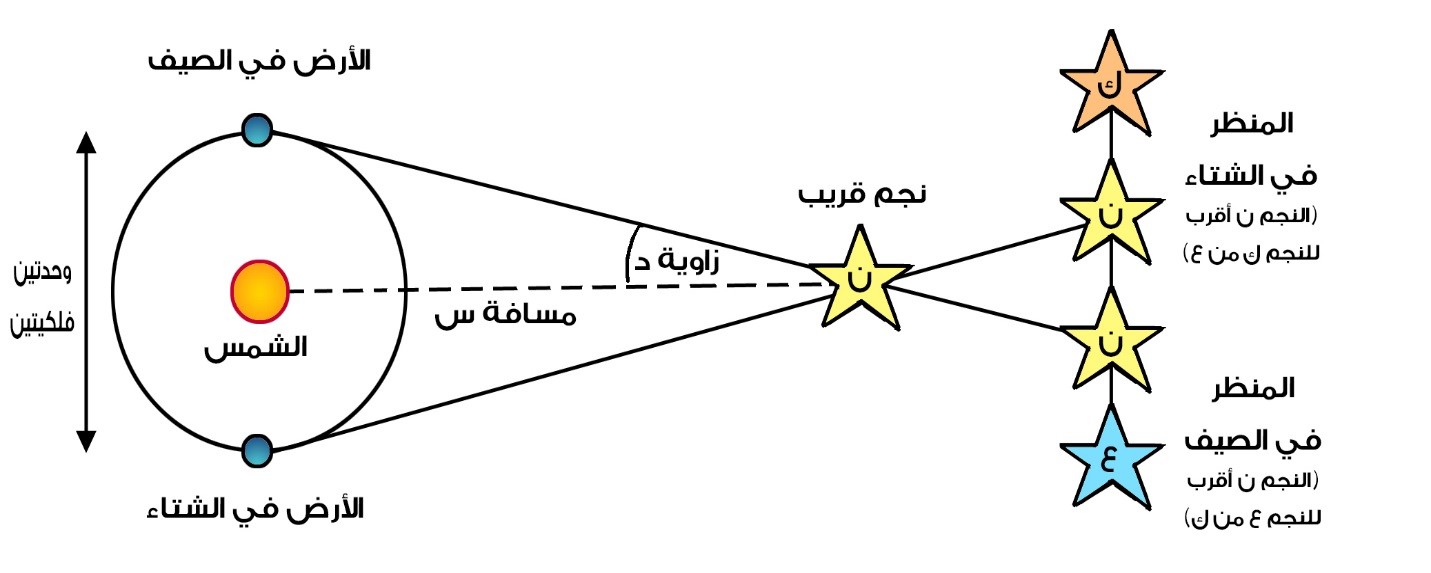
شكل 2: فكرة التخاطل.
ظاد = 1 و.ف./ س
حيث ظا هي ظل زاوية التخاطل (المقابل/المجاور)، د هي زاوية التخاطل، 1 و.ف. هي مسافة الوحدة الفلكية المعروفة، وس هي المسافة المراد حسابها. وبما أن زاوية التخاطل صغيرة في الغالب، يستخدم الفلكيون ثانية القوس كوحدة لقياس زاوية التخاطل. وبمجرد حل المعادلة أعلاه بدلالة س، حيث أن زاوية التخاطل قد تم قياسها مسبقا، يستطيع الفلكيون حساب بعد الأجرام السماوية خارج مجموعتنا الشمسية.
إلا أن هذه الطريقة أيضا محدودة داخل مجرتنا درب اللبانة، إذ تصبح النجوم خارج مجرتنا ثابتة تقريبا ويستحيل قياس زاوية التخاطل، لذا يلجأ الفلكيون إلى الطريقة الثالثة.
3- الشموع المعيارية:
تستخدم هذه الطريقة لمعرفة بعد الأجرام السماوية خارج مجرتنا، حيث تعرّف الشموع المعيارية بأنها نجوم ذات سطوع معروف من على مسافة معينة. تقوم فكرة الشموع المعيارية كالتالي، لنفرض أن لديك مصباح كهربائي ذو إضاءة معلومة وطلبت من صديقك أن يأخذ المصباح ويبتعد عنك، ستلاحظ أن سطوع المصباح يقل مع زيادة المسافة. وقد وجد العلماء أن هناك علاقة بين المسافة والسطوع حيث إن السطوع يتناسب عكسيا مع مربع المسافة (قانون التربيع العكسي)، وبمقارنة السطوع الأصلي للمصباح والسطوع الذي تستقبله من صديقك تستطيع تحديد المسافة بينك وبين صديقك. وفي الفضاء يستعين الفلكيون بنوعين من الشموع المعيارية وهما:
أ) متغيرات سيفيدية
ب) مستعر أعظم من نوع Iأ.
في كلا النوعين يستخدم العلماء الصيغة التالية لحساب المسافات:
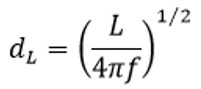
حيث L هي سطوع الشموع المعيارية، و f هو الفيض المقاس أي السطوع الذي نقيسه من النجوم المراد تحديد بعدها عنا، و dL هي المسافة المراد حسابها وتدعى بمسافة السطوع.
أ) متغيرات سيفيدية:
تعرف المتغيرات بأنها نجوم ذات سطوع متغير مع مرور الزمن فقد يتغير سطوعها خلال شهور أو أيام أو حتى ساعات. إلا أن المتغيرات السيفيدية تعتبر مميزة حيث إن سطوعها الداخلي غير ثابت فهي تنتفخ وتتضاءل مثل البالون بوتيرة ثابتة مع مرور الزمن (شكل 3).
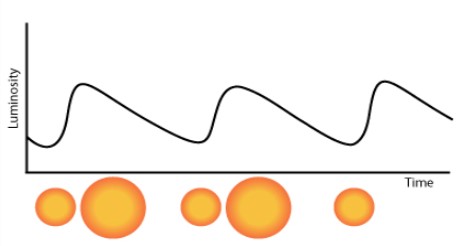شكل 3: التغير الدوري لسطوع المتغيرات السيفيدية مع مرور الزمن.
لكن المتغيرات السيفيدية تسمح لنا بقياس المسافات على بعد 40 مليون سنة ضوئية تقريبا، فبعد هذه المسافة تصبح سطوع المتغيرات السيفيدية مبهمة جدا ويصعب معالجتها، لذا ينتقل العلماء إلى النوع الآخر من الشموع المعيارية.
ب) المستعر الأعظم من نوع Iأ:
تتألف المستعرات الأعظم من نوع Iأ من نظام ثنائي، حيث يكون أحد الأجرام قزما أبيض والآخر عملاقا أحمر (شكل 4). إذ يقوم القزم الأبيض بامتصاص كتلة العملاق الأحمر إلى أن يصل إلى حد شانديراسيخار (وهي الكتلة القصوى للقزم الأبيض المستقر قبل أن يتحول إلى حالة غير مستقرة)، وتقدر بـ 1.4 من كتلة الشمس لينفجر بعدها تاركا العملاق الأحمر طليقا ليصبح نجما حرا. تعد هذه الانفجارات ساطعة جدا لدرجة أنها تضيئ المجرة برمتها (شكل 5).
شكل 4: مستعر أعظم من نوع Iأ.
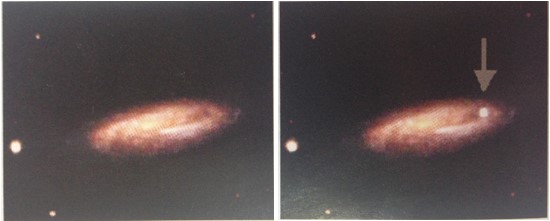شكل 5: (يسار) مجرة قبل انفجار المستعر الأعظم، (يمين) المجرة بعد الانفجار.
يسمح لنا هذا النوع من الشموع المعيارية بقياس المسافات في الفضاء لبضعة مليارات من السنين الضوئية، فأبعد من ذلك حتى هذه الانفجارات الساطعة للغاية تصبح خافتة ولا يمكن رصدها، لذا يلجأ الفلكيون إلى الطريقة الرابعة والأخيرة.
4- الإزاحة الحمراء وقانون هابل:
إذا وقفت بجانب الطريق وكانت هناك سيارة تقترب منك ستسمع صفارتها وهي قادمة نحوك يزداد حدة كلما اقتربت إليك وبمجرد عبورها منك سينخفض صوت الصفارة (البوق) بشكل مفاجئ، يعرف هذا النوع من الظواهر بتأثير دوبلر حيث إن موجات الصوت تنضغط بينما يتجه مصدر الصوت نحوك فيزداد تردده، ويتمدد بينما يبتعد المصدر عنك ويقل تردده. يحدث الشيء ذاته مع الضوء، إلا أن الضوء يغير لونه (الطيف) بدلا من حدته. فإن كان هناك مصدر ضوء يتجه نحوك فإن الطول الموجي لطيفه يتقلص (يزداد تردده) ويتغير لونه نحو الأزرق (الإزاحة الزرقاء)، أما إن كان المصدر يبتعد عنك فإن الطول الموجي لطيفه يتمدد (يقل تردده) ويتغير لونه نحو الأحمر (الإزاحة الحمراء) (شكل 6).
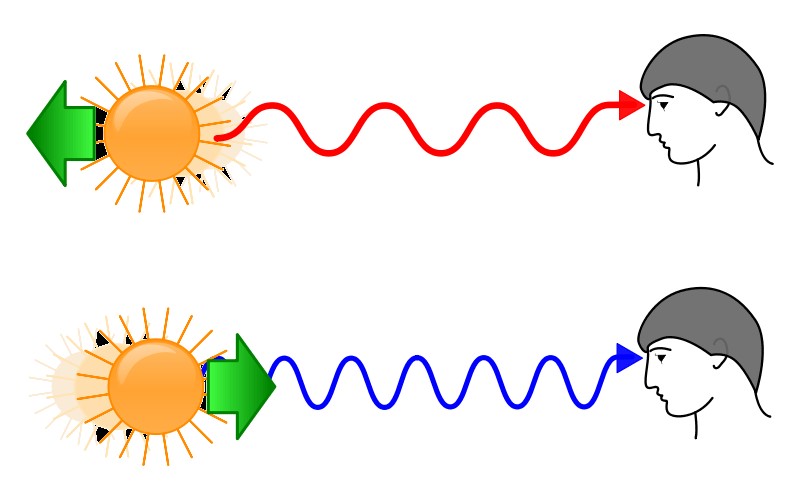شكل 6: الإزاحة الحمراء والزرقاء لمصدر ضوئي متحرك.
وفقا لذلك، فإذا قمنا برصد طول موجي لمجرة ما فإن الطول الموجي المرصود يختلف عن الطول الموجي المنبعث من المجرة، وبمقارنة كلا الطولين الموجيين نحصل على مقدار الإزاحة الحمراء. وفي عام 1929، قام الفلكي الشهير إدوين هابل بقياس الإزاحة الحمراء لخمسين مجرة تقريبا واستطاع بواسطتها تقدير بعد بعض منها ليكتشف أن الكون في حالة اتساع. حيث قام برسم بياني للإزاحة الحمراء مقابل المسافة (شكل 7) ليتوصل إلى علاقته الخطية الشهيرة المعروفة بقانون هابل:
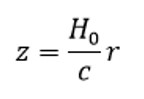
حيث z هي مقدار الإزاحة الحمراء، c هي سرعة الضوء، r هي المسافة المراد حسابها، و H0 هو ثابت هابل ويقدر بنحو 70 كم/ث لكل مليون فرسخ نجمي (1 فرسخ نجمي ≈ 3.26 سنة ضوئية).
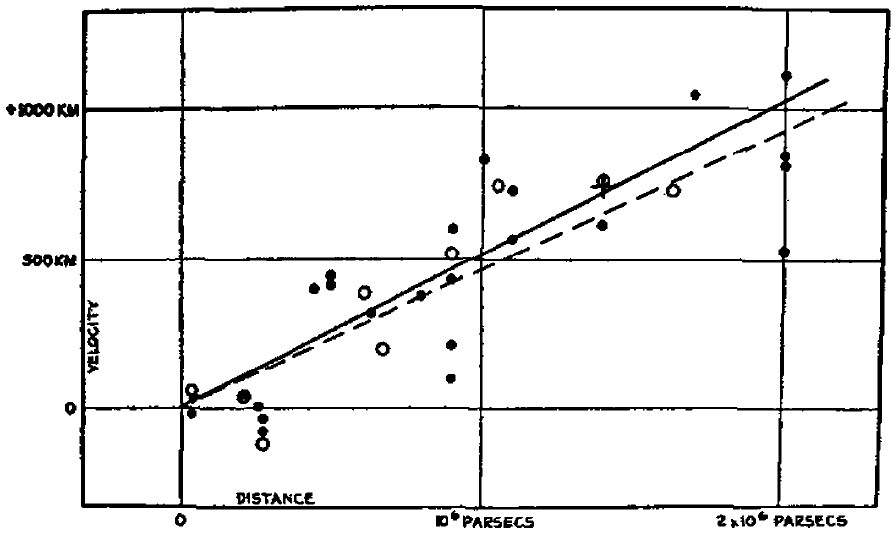
شكل 7: الرسم البياني الأصلي لهابل عن العلاقة الخطية بين الإزاحة الحمراء والمسافة.
الوحدة الفلكية (Astronomical unit)
التخاطل الرياضي (Trigonometric parallax)
ثانية القوس (arcsec)
علم المثلثات (Trigonometry)
الشموع المعيارية (Standard candles)
متغيرات سيفيدية (Cepheid variables)
مستعر أعظم نوع Iأ (type Ia supernova)
قانون التربيع العكسي (Inverse-square law)
القزم الأبيض (White dwarf)
العملاق الأحمر (Red giant)
حد شاندراسيخار (Chandrasekhar limit)
السطوع (Luminosity)
الفيض (Flux)
مسافة السطوع (Luminosity distance)
الإزاحة الحمراء (Redshift)
الإزاحة الزرقاء (Blueshift)
قانون هابل (Hubble’s Law)
الطيف (Spectrum)
إدوين هابل (Edwin Hubble)
تأثير دوبلر (The Doppler Effect)
ثابت هابل (Hubble’s constant)
فرسخ نجمي (Parsec)
المصادر:
- Ryden, B. (2003). Measuring Cosmological Parameters. In Introduction to cosmology. San Francisco: Addison-Wesley.
- Distance measurement in Astronomy. (n.d.). Retrieved November 28, 2015, from http://www.schoolphysics.co.uk/age14-16/Astronomy/text/Measuring_astronomical_distances/index.html
- Radar Basics. (n.d.). Retrieved November 28, 2015, from http://www.radartutorial.eu/01.basics/Distance-determination.en.html
- Light seconds, light years, light centuries: How to measure extreme distances – Yuan-Sen Ting. (n.d.). Retrieved November 28, 2015, from https://www.youtube.com/watch?v=Op3AYaJc0Xw
- Pasachoff, J., & Filippenko, A. (n.d.). Stars: Distance Suns. In The cosmos: Astronomy in the new millennium (Fourth ed.).
